九つの点を折れ線で結ぶ話

発想法の本やセミナーで、3×3に並べられた九つの点を、最も折れ曲がり回数の少ない折れ線で結びなさいという問題が、例としてあげられます。

　　　　　　　　　　　　

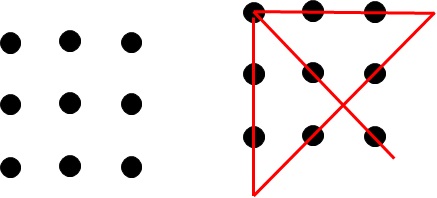
上の図の左が問題で、右が答えということになります。つまり、3回曲がる、4つの折れ線ですね。 で、何でこれが発想法に関係するかというと、最も折れ曲がり回数の少ない結び方は、図の範囲から線がはみ出してしまうんですね。図から線がはみ出てはいけないという条件は、問題には入っていないんですが、人は無意識のうちに、思考に制約を加えてしまう。これを「偽の制約条件」といって、発想を妨げるものと言われています。 ところで、この答えで満足しているようだと、本当の発想法とはいえない、と私は思います。 2回曲がる3本の折れ線で結べないでしょうか？ 点は有限の大きさを持ちますから、横向きに点上を結ぶ3本の平行線を引いて、点の大きさを利用して、上下の二つの線をわずかに右に回転し、中央の線をわずかに左に回転します。そうすると、線は平行でなくなり、どこかで交差します。つまり、2回曲がる、3本の折れ線で、この図の九つの点は結べることになります。

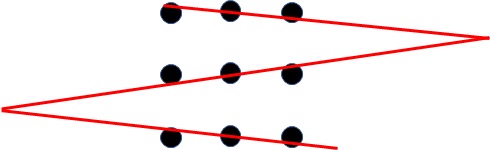
さて、それでは、それ以下の解はないでしょうか？ 実は、単一の直線で図の九つの点を結ぶこともできます。 これには、まず、横向きに3点上を通る3本の平行線を引きます。次に、紙を丸めて、それぞれの直線が、立体的には円となるようにします。それから、紙をわずかにずらし、直線が隣の直線と重なるようにします。そうすると、直線は、立体的には、一本の螺旋のうえに乗ることになります。これは、面内で見ると、一本の直線で九つの点が結ばれた形になっています。 あ、「いんちき」という声が聞こえたみたいですね。この螺旋、直線じゃない、と言いたいのかな？ しかし、何が直線で、何が直線でないかは、定義の問題です。曲面上にも直線は定義できますからね。 一般相対性理論の教えるところによれば、われわれが住むこの空間も曲がっているそうです。しかし、曲がった空間の中で、光は直進するんだそうですよ。つまり、直線があるんですね。 また、現実的な応用を考えるときも、たとえばフレキシブル基板等は、自由に曲げて組み立てることができます。そのような条件下では、上の解もアリということになります。 問題に対する制約条件、常識で決めてはまずいんじゃないでしょうかね。 そういう意味では、発想法のたいてい本は「落第」！！