WordPressには、アクセスを集めている記事の上位30ページを集計する機能があります。32%ともっともアクセスを集めているのがトップページなのは当たり前の話かもしれませんけど、長きにわたって3-4%付近のアクセスを集めて第2位となっているエントリーが「虚数時間の物理学:ローレンツ変換とミンコフスキー空間」です。これ、2016年11月の記事で、5年も前の記事なのですね。あれから長い時間もたったことですし、本日は多少の時間もとれますことから、このあたりで、多少の解説を追加しておくこととします。(本エントリーは、1/6付け「ローレンツ変換と天動説」、1/12改題「虚数時間とファインマン氏の憂鬱」を改めて投稿するものです)
(2025.1.5:Caltechサイトの”The Feynman Lectures on Physics”へのリンクを追加しました。)
ローレンツ変換と回転変換の関係
ローレンツ変換と回転変換の二つの式に関して、ファインマン物理学〈1〉力学では以下のように記述しております。(原文はこちらです。)
“静止している” 観測者位置と時間 $(x, y, z, t)$ と、速度$u$で “運動している” 宇宙船の中の位置と時間 $(x’, y’, z’, t’)$ との間の関係を示すローレンツ変換は、
$x'= \frac{x-ut}{\sqrt{1-u^2/c^2}}$$y'=y$$z'=z$(17.1)$t'=\frac{t-ux/c^2}{\sqrt{1-u^2/c^2}}$である。また方程式(11.5=17.2)も、二つの座標における測定の関係を述べたものであるが、それはそのうちの一方が、他のものに対してある角度だけまわった場合である。
$x'=x \cos{θ}+y \sin{θ}$$y'=y \cos{θ}-x \sin{θ}$(17.2)$z'=z$(17.1) と (17.2) とをくらべてみる。(17.2) の場合には、太郎の x 軸と次郎の x’ 軸との間の角が $θ$ であって、そういう軸によってそれぞれ測定が行われているのである。(17.2) のどの式をみても、“ ’ のついている” 量には、“ ’ のついていない” 量がまじりあっている。新しい x’ には、x と y とがまじりあい、新しい y’ にも、x と y とがまじりあっている。
......
このような見方でローレンツ変換を見ることはできないだろうか? ローレンツ変換には、位置と時間とがまじり合っている。空間測定と時間測定の間に差があるが、その差によって新しい空間測定が生ずる。いいかえれば、1人の観測者の空間測定を他の観測者からみれば、時間がちょっとまじりこむ。
ここで、ファインマンはローレンツ変換の式と回転変換の式を並べて表示して、これらがよく似ている、どちらも「量がまじりあっている」と述べます。でもこの二つの式は、サイン、コサインがタンジェントでどう表されるかを知っている人だと、「まじりあっている」以上の類似性をすぐに見抜いてしまうのですね。
具体的な式の変形は「 虚数時間の物理学:ローレンツ変換とミンコフスキー空間 」に示しましたけど、これら双方の式の違いは「時間の項が虚数になっていることだけだ」と気付くのにそれほど時間はかかりません。つまり、$s = \tan{θ}$ を用いて表すと、サイン、コサインは次のようになりますから。これと上の二つの式を眺めれば、なんとなく見えてくるのではないでしょうか。
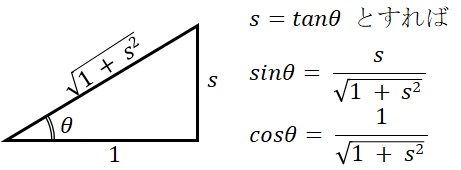
実は私、三角関数を扱う仕事をしていた時、この本をたまたま読んで、これはおかしい、誰も気づいていないのはなぜだろう、と疑問を持ち、当時扱っていたJunetのニュースグループ“fj.sci.physics”で質問をしてみたのですね。そこで返ってきた答えがパウリの相対性理論を読んだらどうか、ということで、読んでみたらあらびっくり、最初はそういう扱いをしていたということ。(同書は現在では相対性理論〈上〉 (ちくま学芸文庫)、相対性理論〈下〉 (ちくま学芸文庫)、二冊の文庫本で出ています。けど、上巻が無茶苦茶高いのはなぜでしょう。お気を付けください。)
それにしてもファインマンがこの二つの式を並べて示した時、カルテックの学生たちは、誰もこれらの式がほとんど同じであることに気付かなかったのでしょうか? 私には、その時発したファインマンの心の声が聞こえるような気がいたします。「お前ら、気付けよなあ」と。もしもカルテックの学生たちが気づかなかったと致しますと、この大先生、そんなことを思いながら、この二つの式を並べていたのではないかな?
時空の虚実
ファインマン物理学〈1〉力学 (p241)には、次のような興味深い記述もあります(適宜改行を補いました)。(原文はこちらの、17-2の最後に近い部分です。式番号(17.5)を探してください。)
$t'^2-x'^2-y'^2-z'^2 = t^2-x^2-y^2-z^2$(17.5) 時空間と普通の空間とのちがい、インタバルと距離の関係は、実に面白い問題である。
式(17.5)によると、ある座標系における点が、時間がゼロで空間だけがあったとすると、インタバルの自乗は負になり、インタバルそれ自身は負数の平方根で虚数になる。この理論によれば、インタバルは実数にもなれるし、虚数にもなれる。インタバルの自乗は正にも負にもなれる。
これは、距離の自乗が常に正であるのとはちがう。インタバルが虚数である場合には、二点の間のインタバルは空間的であるという。(虚数とはいわないで。)それはこの場合のインタバルは、時間によりも空間に似ているからである。また、二つのものが一つの座標系で同一の場所にあるが時間的にちがうという場合には、時間の自乗は正で距離はゼロで、インタバルの自乗は正である。これを時間的なインタバルという。
ここでは、3次元空間に対して「距離」(ディスタンス、かな?)という言葉を用い、4次元空間に対しては「インタバル(間隔)」という言葉を用いております。確かに、インタバルという言葉には時間間隔という意味合いもあり、これに対して「距離」の方は道程のような空間的な長さを表すように思います。まあ、後者は心理的な離れ具合を指す言葉にも使いますけど、これはこの際おいておきましょう。
でも、純粋に物理的に言えば、距離も間隔も同じ話であって、二点間の位置ベクトルの差の大きさが距離でありインタバルなのですね。ベクトルの大きさを自乗したものは、ベクトルの自分自身とのスカラー積で与えられます。これは、座標をテンソル表現した際には、一階のテンソルの縮約であり、3次元も4次元も扱いは同じなのですね。
問題は、4次元世界の場合、時間と空間に実数・虚数の差が生じるということ。上のファインマンの主張では、インタバルが虚数の場合、インタバルは空間的であるといい、虚数とは言うなといたします。一方、インタバルが実数の場合は、インタバルは時間的であるというのだといたします。虚数を虚数というなとは、無茶苦茶な主張であるとは思いますが、虚数・実数の違いが、時間的・空間的の違いに対応するという点は、ミンコフスキーのやり方と何ら変わらないのですね。
ここで、ミンコフスキーは時間を虚数としているのに対し、ファインマンは、空間を虚数に割りあてている。確かに、時空の間に虚実の差を設ければそれでよく、いずれを実数とし、いずれを虚数とするかは任意ではあります。でも、空間的な離れ具合を虚数とするやりかたでは、そのままでは面積がマイナスになるという問題が生じます。また、量子力学の状態ベクトルの表現とも食い違いが生じてしまいます。ここは、当初のミンコフスキー流のやり方を継承して、時間を虚数とするのが妥当ではないかと思います。
このような問題は容易に予測されるにもかかわらず、ファインマンたちが空間を虚数に割りあてたのはなぜか、これも一つの謎ではあるのですが、ミンコフスキーの虚数時間との差を明確に出そうとすれば、空間を虚数に割りあてるしかなかったのではないか、という気も致します。こうしておけば、ミンコフスキーとの違いは、時間と空間のいずれを虚数に割りあてるかという違いになり、形の上では対等になります。
もちろん、こんなところでどうしようと、そこに虚実の違いは厳としてあり、これを同じとするのか、違うとするのかが、ミンコフスキーとファインマンの最大の差であることに違いはありません。その違いというか、優劣の差が、「虚数を虚数と呼ぶな」という無理な注文に表れてしまった。これが現実だというしかありません。
状態ベクトルの時間反転:量子力学
時間が虚数的にふるまうという考え方は、量子論が物理状態を扱う時に使われております状態ベクトルに対して時間反転操作をすると「共役になる(虚数部の符号が反転する)」という事実からもサポートされるのですね。
たとえば、「ワインバーグ場の量子論 (1巻) (物理学叢書 (75))」の70ページには次の式が掲げられております。
ここで、 $Φ$と$Ψ$は物理的状態を表す「状態ベクトル」で、ヒルベルト空間(スカラー積が定義された複素ベクトル空間)中のベクトルとして与えられております。この2.1.1式は、物理的状態の順序を逆にしたもの(時間を反転したもの)は、共役になるといっているのですね(「*」で表示)。
これがどういうことか、ちょっと考えてみますと、共役とは、複素数の虚数部の符号が反転したものを言いますから、時間を反転すると虚数部の符号が逆になる。「時間成分は純虚数として状態ベクトルに含まれている」、といっているの同じことなのですね。ここまで言って、なぜミンコフスキーを受け入れないか、全く理解に苦しみます。
このような物言いは、ワインバーグに限らず、たとえばファインマンも行っております。「ファインマン物理学〈5〉量子力学」では、シュテルンゲルラッハの装置を用いた実験に対する考察から、状態ベクトルに時間反転操作を施すと共役になることを証明しているのですね(最後の式がワインバーグの2.1.1式に相当します)。これは、時間の虚数性を証明しているともいえるような論理です。この議論は、74ページから続いているのですが、長くなりますので、ここでは89ページのコピーだけを示しておきます。(原文はこちらです。)

89ページの最初の部分とその脚注には、なかなか含蓄があります。ファインマンはこう述べているのですね。
全ての法則がその結果として導かれるような最小限の独立な公理系を見つけるという数学的な問題に特に興味を持っているわけではない†。そこでここでは、完全にして、かつ明らかに矛盾を含むことのないような法則を知れば、それで満足しておくことにする。
† 不要かつ余計な真理などにかまうな!
ここでファインマンが表明しているのは、「最小限の独立な公理系を見つけるという数学的な問題」は「不要かつ余計な真理」だというのですね。確かに物理現象を説明するという目的からは、最も単純な原理に帰着する必要はない。でもそれって、天動説もそうであったのですね。そしてニュートンの大発見は、月もリンゴも同じ万有引力によって地球に引かれているという点にありました。最小限の法則を見出すことこそ、物理学の神髄だったはずです。
ローレンツ・ポアンカレの相対性理論
(この節は、1/8追記)実は、アインシュタインが相対性理論を発表する前に、ローレンツ・ポアンカレの相対性理論と呼ばれた理論があったのですね(本ブログのこちらのエントリーで紹介しております。)
この理論は、当時宇宙に充満していると考えられていたエーテルに対する地球の運動が検出されない理由をローレンツ収縮という形で十分に説明するものでした。上のファインマンの要求には、 ローレンツ・ポアンカレの相対性理論 も完全に応えているのですね。
以前のエントリーに紹介した広重徹「相対論はどこから生まれたか」(日本物理学会誌26巻6号p380 (1971))には、このあたりの事情を以下のように解説しております。
確かにそれ(ポアンカレ-ローレンツの相対性理論)は相対論とよびたくなるような理論であった。数式の面から見ると、それは相対論と同じ形をしている。その上ポアンカレはしばしば、“相対性原理”ということを唱えている。
しかし見落としてならないのは、それで彼が意味したのは、対エーテル運動の実験的検出不可能性のことだったということである。
ポアンカレにとって、それは理論からの帰結として説明されるべきもので、アインシュタインにおけるように、その上に全理論が築かれる構成的原理ではなかった。ローレンツ-ポアンカレの理論はあくまで、生じているはずの効果が表に現れないことを説明する理論だったのである。この点がそれを、すべての慣性系の同等性という原理から出発する相対論から、決定的に区別するものである。
しかし、ローレンツ-ポアンカレの理論は、生じているはずの効果が表に現れないのはなぜかという、人々が長年追求してきた問題には完全に答えるものであった。当時の人々の問題意識からすればそれでことは落着したのであって、その上アインシュタインに俟つものは何もなかった。
じっさい、1905年以後しばらくの物理学者たちの議論を読んでいると、彼らはローレンツ理論を正統として受け入れており、アインシュタインの名は、同じことを多少違った形で表現した人としてあげるに過ぎない。
アインシュタインの理論の革命性をはじめて明瞭に指摘したのは、ミンコフスキーであった。ローレンツとポアンカレは、前者ははっきりと明言し、後者は完全な沈黙によって、アインシュタイン理論への不同意を表明していた。
結局のところ、アインシュタインの相対性理論の重要なポイントは、まさにファインマンも指摘しているように、「時間と空間が混ざり合う」という点であって、これは、われわれが時間と空間を一体とした四元時空に生きており、異なる速度で運動する他の慣性系への座標変換は、時間を含む空間の回転変換に他ならない、という点にあるのでしょう。そしてこの視点を明瞭に与えたことがミンコフスキーの功績である、と評価すべきなのですね。
異なる慣性系への座標変換を回転変換と同一視するためには、時間と空間に虚実の違いを認めることが必須です。ファインマンも時空の間に虚実の違いがあること自体は認めているのですが、ローレンツ変換の式を回転変換の式に帰着することは断固として拒否しているのですね。そして、「最小限の独立な公理系」は「不要かつ余計な真理」などというのですが、こういう行為に対しては、20世紀に入って人類が獲得した一つの知的水準から19世紀の知的水準に後退する、野蛮な行為だというしかない。
それは、ファインマン自身が講演で非難したソ連の野蛮な行為と同種のものだというしかないし、ナチスによるユダヤ系知識人に対する迫害や、中国の焚書坑儒と、根は同じ行為であるというしかない。ファインマン自身がこのようなやり方を嫌っていることは、ファインマン物理学にもいくつかみられる(そしてその一部は本エントリーでも紹介している)不思議な記述*から推察されるのですが、結局は加担しております。
確かに冷戦時代、東側の科学者を持ち上げるような行為は、西側陣営の威厳を損ね、市民の不安を募らせる利敵行為でもあったでしょう。政府ともつながりの強かった当時の物理学者には、少々公正さに疑問を抱かせる行為であっても、このような利敵行為に手を染めるわけにはいかない事情も分かるのですね。
でも、冷戦時代が過去のものとなった現在において、このあたりの考え方は見直されてもよいのではないか。むしろ、こういう歪みを正すことこそ、今の物理学者には求められているのではないか、私はそう思うわけです。(1/8の追記は、ここまでです)
*: 不思議な記述といえば、Ⅳ巻65ページの次の部分も不思議な記述です。無人島でもローレンツ変換を忘れるはずはないとは、いったいどういう意味なのでしょう!? まるで、強迫概念のようです。(原文はこちら、図26-2の後です。)
任意の運動をする1個の電荷によるポテンシャルの式を得た時、我々は完全な電気力学を得たことになる。任意の電荷分布によるポテンシャルは、重ね合わせによって与えられる。故に、すべての電気力学的現象は、マクスウェル方程式を書き下すか、あるいは次のいくつかの注意書きによって総括されるわけである(無人島に置かれたとしても、これらを思い出せば、そこからすべてのことが導き出せる。もちろん、ローレンツ変換はわかっている。無人島であろうと、どこであろうとこれをわすれる筈はない。)
消されたミンコフスキー
時間を虚数として空間と同様に扱おうというミンコフスキーのやり方は、相対性理論が登場した後のしばらくの期間は物理学の世界の主流でもありました。実は、1960年代の初めごろまでは、ミンコフスキー流の扱いも一般的に行われておりました。 「虚数時間の物理学:ローレンツ変換とミンコフスキー空間」 にも書きましたように、1920年出版のマックス・ボルン著「アインシュタインの相対性理論」(解説はこちら)やパウリ著「相対性理論(上)、(下)」(ドイツ語で書かれた原著は1921年、英語版は1956年の出版。解説はこちら)なども、ミンコフスキーの座標系に基づいて記述されました。
しかしながら、1960年前後からミンコフスキー流のやり方は影を潜めてまいります。ファインマン物理学は、日本語版が1967年、英語版が1963年の出版で、1961年から1962年にかけてファインマンがカルテックで行った講義に基づいて書かれております。この内容は、上で紹介しましたように、ローレンツ変換を前面に出し、ミンコフスキーのミの字も出てこないやり方となっています。
この大きな変化がなぜ起こったのか、虚数が出てくることは隠しようもないのですが、その場合もなぜ時間を実数として空間的長さを虚数とするのか、そんなことをすると、面積が負になるなどの困ったこともあるにもかかわらずそうするのはなぜか、疑問は尽きないのですね。
もちろん、邪推ならすぐに出てくる。つまり、当時はソ連圏でありましたリトアニア生まれのミンコフスキーが物理学の根幹部分に現れるなど、英米の学者としては認めるわけにはいかない、という邪推ですね。なにぶん当時は、核兵器で互いに威嚇する東西対立の時代。核エネルギーがかくも巨大である理由が、 E = m c2 という、相対論から導き出された式で説明されていたこともあったのですね。この式は正しい、だけど実際のところこの式で核エネルギーが解放されるわけでもないのですが。
もう一つは、科学の世界にもナショナリズムがあって、米国籍の日本人のノーベル賞受賞を日本国民が喜んだり、(米国の天文学者が発見した)冥王星が惑星の座から引きずり降ろされる時に米国の天文学者が抵抗したりするのも、ナショナリズムのなせる業。前者は微笑ましい話でしょうけど、後者は科学者の態度としては少々難があります。
西側世界の科学者としては、リトアニア生まれの物理学者を持ち上げる理由は全然ないし、引きずりおろす理由は山のようにある、ということでしょうが、その結果、物理学の正常な発展が歪められたと致しますと、これは人類知性の発展に、大きな害があったというしかありません。
形而上学(メタフィジックス)的アプローチ
虚数時間を受け入れない理由として、実数は実在するけど、虚数は想像の産物である、といった主張もあります。でも、そういう言い方をするなら、実数も想像の産物なのですね。実数も虚数も、自然数さえも、言語と同じ、人間精神が生み出したもので、それに対応する自然界の事物はあったとしても、その対応関係ははなはだあやふや。冥王星が数に含まれるかどうかは、結局のところ認識の問題、定義の問題、あるいは、政治的問題ですらあるわけで、自然界に確固とした(惑星の数を表す)自然数があるわけではない、人が適当に対応関係を付けているだけの話なのですね。
まあ、虚数はイマジナルで、実数がリアル。それは言葉の意味としては正しいけれど、現実を反映している姿ではない。少なくともそれが時空の虚実を定める根拠にはなりません。
数のみならず、物理法則を含む物理学を含めて、学問なるものはすべてが人の精神的働きが生み出したもの。それは自然界を描写したものであることは確かなのでしょうが、自然界そのものでも、自然界に実在するものでもない、人間精神の産物なのですね。そして、その際の描写に適した記号なら、どんどん受け入れていけばよいわけです。
ファインマンは「全ての法則がその結果として導かれるような最小限の独立な公理系を見つけるという数学的な問題に特に興味を持っているわけではない」と主張します。そして、「不要かつ余計な真理などにかまうな!」と強調するのですが、学問というものは、実は「不要かつ余計な真理の追究」なのではないのか。私にはむしろそう思われるのですね。
ここは、 物理学においても、「全ての法則がその結果として導かれるような最小限の独立な公理系を見つけるという数学的な問題」に取り組みたいところ。それこそが、哲学(知を愛する学)としての物理学、ニュートンの言葉では「自然哲学」の、あるべき姿ではないかと思います。
付:「知能低下の人類史」より
エドワード・ダットンとマイケル・A・ウドリー・オブ・メニーの知能低下の人類史: 忍び寄る現代文明クライシスは、興味深い書物なのですが、その最初に近い部分に次のような記述があります。
科学では、できるだけ少ない限定からできるだけ多くを説明できる理論が求められる。オッカムのカミソリとは、イギリスの修道士ウィリアム・オッカム(1287-1347頃)にちなんだものだが、もっとも単純な理論が最高のものであることは、すべての科学者が信奉する定理である。もし二つの異なった出来事が一つの理論でうまく説明できるなら、それぞれに異なった理論を持ち出すよりも望ましい。
われわれが本書で示すのは、もっとも少ない仮説に基づくもっとも単純な説明である。人類が月に戻れなくなったことや、コンコルドを飛ばせなくなったのは、我々がだんだんと知的に退行しているからなのだ。これ以外の理由でも、一つ二つの事件やそれらの諸側面を説明できるかもしれないが、それらにはすべてに納得できない疑問や根拠のない仮定がつきまとう。本書での説明には、そうした問題は存在しない。
この最初のパラグラフは、まさに、ファインマン氏の主張を真っ向から否定するもので、「まあ、ふつう、そうだよなあ」としか言いようもない、あたり前の主張であるように思われます。つまり、ファインマン氏の主張は奇異である、ということですね。
この第二パラグラフに関しては、評価を保留しておきましょう。確かに人類は徐々におろかになっている。でも、月に行ったりコンコルドを飛ばしたりしたときの人類が最も賢かったかといえばそうでもない。1910年ごろの人類が、最も賢かったような気がしないでもありません。このあたりにつきましては、またいずれかの機会に議論いたしましょう。(本節は、2022.1.17に追加しました)
参考:関連するエントリーとその概要
このテーマに関しては、一連のエントリーで様々な角度から扱ってまいりました。ここで最も興味を引いた点は、アインシュタインが特殊相対性理論を発表した直後は、これをミンコフスキー流の四次元の幾何学(時間を虚数とする)で説明することが主流だったのだが、その後、ミンコフスキーの流儀は廃れ、時間を実数とするローレンツ変換で説明するようになったのはなぜか、という問題です。
古い相対論解釈に関しては、マックス・ボルン著「アインシュタインの相対性原理」でも紹介されており、本ブログでもエントリー「ボルン著『アインシュタインの相対性理論』を読む」で取り上げております。
この話題に関する本ブログの纏めのエントリー 「虚数時間の物理学:ローレンツ変換とミンコフスキー空間」 では、ローレンツ変換とミンコフスキー流の扱いは、数学的には、何ら変わらないということを、回転変換の公式からローレンツ変換の公式を導き出す形で説明しております。つまり、数学的には、ローレンツ変換も、ミンコフスキー空間も、何ら変わらないということなのですね。
こうなりますと、次の謎が出てまいります。なぜ時間を虚数にするという流儀は忘れ去られてしまったのか、ということですね。
一つの可能性は、電磁気学なり、量子力学なりに展開する際に何らかの問題が生じたということ。そこでまずは、電磁気学について検討してみました。その結果は、ブログエントリー「虚数時間の電磁気学」にご紹介しました。このページ、途中で符号の付け方を間違えているのですが、基本的な論理展開は問題ないはず。つまり、時間を虚数としても電磁気学は何ら問題ない。むしろその方が、スマートな記述が可能になるのですね。
では、量子力学はどうか、ということで考察した結果が「虚数時間の物理学、さて、量子力学は?」でして、驚いたことに、量子力学の公式に表れる虚数が時間を虚数とすることで消えてしまう。量子力学の諸公式に虚数が現れていたのは、実は、時間が虚数であったからだ、という事実なのですね。
また、重力理論はどうなるかといいますと、そもそも、アインシュタインが一般相対性理論を導いたのがミンコフスキー流の虚数時間に依っており、この展開は、パウリの「相対性理論」でも扱われています。(同書は、後に文庫化され、相対性理論〈上〉 (ちくま学芸文庫)、相対性理論〈下〉 (ちくま学芸文庫)と出ておりますが、こちらも絶版中で、古本に極めて高い値がついております。)
なお、一般相対性理論(重力理論)の展開に用いられておりますテンソル表現に関しても、ミンコフスキー流の虚数時間を用いると物理的意味付けが分かりやすくなる一方で、ディラック流の、時間も空間も実数とおくやり方は、テンソル化の部分で(時間項のみ、共変と反変で符号を変えるという)不自然な約束事を追加する必要が生じます。テンソルと虚数時間の問題に関しては、「テンソルによるベクトルの数値表現と虚数時間」で議論しています。
実は、ディラックの「一般相対性理論 (ちくま学芸文庫)」は、虚数時間を使用せず、空間成分のテンソル化の際に反変と共変に異なる符号を与えるという根拠不明の約束(「ローレンツ変換に対して不変に保つ」でしょうか?)により、計量テンソルの対角成分の符号を時間と空間で反転させているのですが、これは、(直交座標系における計量テンソルの対角成分は基底ベクトルの大きさの自乗ですから)空間方向のベクトルの大きさを虚数としていることと何の変りもないのですね。逆に言えば、虚数時間に基づく場合も、ディラックの一般相対性理論の数式展開がほとんどそのまま使えます。ミンコフスキーの座標系に合わせるためには、符号は反転しなくちゃいけないのですが。(2022.1.22追記)
結局のところ、時間を虚数とするミンコフスキーのやり方は、何ら問題はないし、その方がすっきりとした扱いが可能になる。この一連の議論の中で、種々の形で参照した「ファインマン物理学」の記述を改めて眺めますと、ファインマンの不自然な物言いが目につきます。この面からまとめて本エントリーといたしました。