このブログで時々アクセスされるページに、虚数時間の物理学に関するページがあります。このブログでは、かなりバラバラにこのテーマを扱っておりましたので、このあたりで簡単にまとめておきたいと思います。なお、新しいまとめ「虚数時間とファインマン氏の憂鬱」（修正しました：2022.1.22）を2022.1.6に追加しております。
ローレンツ変換とミンコフスキー空間：数学的には同じ、ということ
空間と時間は一体で取り扱うことができる、三つの空間軸に一つの時間軸を加えた四つの次元の空間に我々は生きている、これがアインシュタインの特殊相対性理論の帰結でした。
互いに異なる速度で移動している人からみた世界、つまりは原点が異なる速度で移動している座標系間での座標変換は、時間軸と（移動方向である）一つの空間軸で作られる面の中での座標の回転変換に他ならないのですが、この変換は空間内の面の中での回転変換とは異なり、ローレンツ変換の形で与えられなければいけません。
ローレンツ変換の公式は、次の形をしております。
(1) x' = (x - u t) / √1 - u2/c2
(2) y' = y
(3) z' = z
(4) t' = (t - u x / c2) / √1 - u2/c2
一方、空間内での回転変換の公式は、次の形をしております。
(5) x' = x cosΘ + y sinΘ
(6) y' = y cosΘ - x sinΘ
(7) z' = z
(8) t' = t
この二つの公式は、ずいぶんと異なっておりますが、三角関数をタンジェントで表すと、つまりs = tanΘを用いて表すと次のようになります。
cosΘ = 1 / √1 + s2
sinΘ = s / √1 + s2
これを(5)式と(6)式に代入すると、次のようになります。
(5') x' = (x + s y) / √1 + s2
(6') y' = (y - s x) / √1 + s2
ここで、yとsを虚数とすれば、すなわち、y = i c t、s = i u / cと置き換えるならば*、これらの式は次のように変形されます。
(5'') x' = (x - u t) / √1 - u2/c2
(6'') y' = i c t' = (i c t - i u x / c) / √1 - u2/c2
(6''')t' = (t - u x / c2) / √1 - u2/c2
(5''), (6''')と(1), (4)式は、同じものとなります。
アインシュタインの特殊相対性理論の帰結は、時間軸と空間軸が互いに影響を及ぼし合うということであり、その関係はローレンツ変換の公式で記述されるということであったのですが、時間が虚数的に振る舞うと仮定すれば**、これらの関係は空間座標における回転変換と何ら変わらない、アインシュタインの特殊相対性理論は四次元空間中の幾何学に他ならない、これがミンコフスキーの得た結論でした。
*：回転は左回転が正であるのに対し、正の速度で移動している座標系への変換は右回転となるため、回転方向を合わせるために速度にマイナスの符号を付ける必要があります。つまり、s = -u / (i c)となります。この分子分母をiで除し、簡素化して表示しています。（この議論は、共通の空間軸であるX軸を横軸にとり右を正とすること、Y軸とt軸は縦軸にとり上を正とすることを前提としています。）
**：時間軸を虚数とする代わりに、空間軸をすべて虚数とする虚数空間でも、同じ形となります。
ミンコフスキー的取り扱いの妥当性
アインシュタインの特殊相対性理論、あるいはローレンツ変換が、三つの空間軸に時間軸を加えた四次元の世界の幾何学で表される（時間軸は、なぜか虚数的に振る舞うのですが）ということを見出したのがミンコフスキーで、この空間をミンコフスキー空間と呼びます。
アインシュタインの特殊相対性理論だけであれば、これはローレンツ収縮を別の言葉で言い換えただけであるようにも受け取られてしまうのですが、これが空間の性質である、われわれは四次元空間の中で生きているのだ、ということは、人の世界観に変革を迫る、大きな発見であったわけです。
ミンコフスキー流の空間の取り扱いは、アインシュタインが重力理論（一般相対性理論）の研究に取り入れ、大きな成功を収めております。また、特殊相対性理論は、元々電磁気学がニュートン力学に矛盾するところからスタートしており、ミンコフスキー流の時空の扱いは電磁気学の法則をシンプルな形で矛盾なく記述します。これにつきましては、本ブログの「虚数時間の電磁気学」で解説いたしました。
2019.1.7追記：一般相対性理論では座標のテンソル表記ということを行っています。この手法は、こちらで解説しましたように、互いに異なる方向を向いた基底ベクトルを用いた二種類の座標表現を用い、最終的には基底ベクトルとは独立したパラメータを得るという手法がとられます。
この時、座標系を特徴づけております計量テンソルの各要素は、基底ベクトルのスカラー積で与えられるのですが、共変テンソルと反変テンソルの要素の符号を入れ替えるというルールを天下り的に与えるようなやり方ですと、このあたりをきちんと説明することができない、という問題もあります。（以下、2/14に追記しています。詳細はこちらをご参照ください。）
ベクトルは、反変テンソルと共変テンソルという二種類のテンソルにより座標表示することが可能です。反変テンソルは、ベクトルを基底ベクトル（直交座標系なら、X軸、Y軸、Z軸方向の単位ベクトルe1、e2、e3）の線形結合で表した際の係数を座標値とする方法で、下式を満足するxkがこれにあたります。
なお、上の式の一番右側はアインシュタインの縮約記法で、同じ上下の添え字を次元の数だけ振って計算した合計をとる（中央の式のようにする）ことを意味します。
共変テンソルはベクトルと基底ベクトルのスカラー積により座標値を得る方法で、下式によりxjが与えられます。これも縮約記法と同様で、jを1から3まで振った三つの式を表しています。
共変テンソルの定義式に反変テンソルの定義式を代入すると下式が得られます。
これは、xkをxjに変換する式で、変換係数 gjk = ej・ek を計量テンソルと呼びます。
時間を含む4元ベクトルでは、添え字をゼロから始め、添え字0を時間に対応する値とします。直交座標系を採用する場合、計量テンソルの非対角成分はすべてゼロとなります。対角成分は、空間部分と時間部分の符号を反転する形で大きさ1の値をとります。
具体的には、g00が-1ならg11 = g22 = g33 = 1、g00が1ならg11 = g22 = g33 = -1とします。ディラックは後者を採用しているのですが、ここでは、より簡素な形に式を書き下すことができる、前者を採用することとします。この場合、計量テンソルの時間部分の対角成分は以下のようになります。
ベクトルのスカラー積は、ベクトルの大きさの積に双方のベクトルのなす角のコサインを乗じたものですから、同じベクトルのスカラー積は、ベクトルの大きさの二乗となります。
つまり、4元ベクトルの時間方向の基底ベクトルの大きさは、二乗すると負になる。これは、時間が虚数的なふるまいをすると考えるミンコフスキー流の扱いに整合します。
一方で、虚数時間には触れていないディラックの一般相対性理論の解説は、反変テンソルと共変テンソルをつくる際の符号のつけ方を規定するという形で虚数が表面に出ない扱いを採用しているのですが、実際には虚数時間を前提としております。
そして、反変・共変テンソルの定義と計量テンソルの導出を上の赤字で書いたように書き下すと、この隠された前提は表面に出てしまいます。
これを隠し通すためには、これらの単純な式が出てこない形で分かりにくく説明するしかなく、一般相対性理論がわかりにくい理由の一つでもあるように思います。
このような行為が学問のあるべき姿であるのか、はなはだ疑問であるように、私には感じられます。
次に、量子力学はどうなるかといいますと、まず、以前に議論いたしましたように、シュレディンガーの波動方程式からも、この解を表す波動方程式からも、虚数単位が消えうせます。つまり、これら諸式に表れる虚数単位は、全て時間が虚数的に振る舞うことから生じております。
また、ワインバーグの「場の量子論（一巻）」によれば、状態ベクトルに時間反転操作を施してできる状態ベクトルは、元の状態ベクトルの共役になるとされており、共役複素数とは虚数部分の符号が反転したものですから、状態ベクトルでも時間項は虚数として含まれているであろうと推察されます。
この事実は、こちらでご紹介しましたように、ファインマンも指摘しており、量子力学の世界の常識であるように思われます。このあたり、専門家の方々の認識を知りたいところです。
といいうわけで、ミンコフスキー流の時空の取り扱いは、おそらく今日の物理学のレベルでも、何ら問題を生じないであろうと思われます。これは当然の話であるともいえます。つまり、ミンコフスキー流の扱いは、ローレンツ変換と数学的に異なるものではなく、ローレンツ変換で問題を生じないのであれば、ミンコフスキー流の扱いでも問題は生じないはずなのですね。
ローレンツ変換の不自然さ
今日一般的な物理学は、時間を実数とするローレンツ変換に基づいてさまざまな式が導かれています。しかしながら、このやり方では、ところどころに説明に苦しむ扱いをせざるを得ません。たとえば、四元ベクトルのスカラー積を求める際に、時間項だけ符号を反転する必要があります。また、テンソルにする際には、共変テンソルと反変テンソルで、時間項の符号を変えてやる必要があります。これも、時間の二乗の項の符号が反転するようにしていることに他なりません。
これはなぜかと問われたら、実は時間が虚数的に振る舞うからである、といった答えしか出てこないはずです。ファインマンは、「ローレンツ変換に対して不変となるように式を立てなくてはいけない」といっているのですが、これは符号を反転する物理的理由であるとは言えないでしょう。
さらに極めつけは、四元距離の二乗の符号に応じて空間的または時間的に離れているとしていることです。二乗して負になる数は虚数と呼ぶのが普通であり、二点間の距離が虚数ならば時間的に、実数ならば空間的に離れているとするのが自然な考え方でしょう。
ファインマンは四元距離に関して、二乗した値が負になってもそれを虚数と呼ぶなと書いているのですが、これは極めて奇妙な物言いです*。
時間を虚数としない一つの理由は、虚数は頭の中で考えられた数であり、実在するものではない、とする考え方があります。しかしながら、実数にしたところで、自然界に実在するものではなく、人が頭の中で考えた数に過ぎません（参照。）
虚数を物理法則から追放しようとしたところで、量子力学の諸公式には虚数単位が多く含まれてしまいます。そしてその虚数単位は、時間を虚数とすることで消し去ることができます。虚数を時間の中に閉じ込めてしまう方が、物理法則ははるかにシンプルに表現できるのですね。
*：ファインマン物理学にはもう一つ奇妙な記述があります。ローレンツ変換の公式は、たとえ無人島に一人流れ着いたときであっても忘れてはいけない、と。このような奇妙な記述が散見される背景には、ファインマンはローレンツ変換に基づくことの不自然さに気付いていたが、これを公に語れない事情があったのではないか、と私は憶測しています。
なぜミンコフスキーは嫌われたか
なぜ、ミンコフスキー流の扱いが一般的でないか。これは大いなるなぞであるように私には思われるのですが、思いつきましたただ一つの理由は、「ミンコフスキー」というその名前が嫌われたということ。
実は、1960年代の初めごろまでは、ミンコフスキー流の扱いも一般的に行われておりました。たとえば、1920年に出版されましたマックス・ボルンの「アインシュタインの相対性理論」（解説はこちら）やパウリの「相対性理論（上）、（下）」（ドイツ語で書かれた原著は1921年、英語版は1956年の出版。解説はこちら）なども、ミンコフスキー流の扱いに基づいて解説しております。
しかしながら、その後徐々に、ローレンツ変換に基礎を置く扱いが一般的となっております。
この変化が起こりました時代は、東西冷戦の時代にあたります。西側と東側が互いに相手を威嚇するのに用いられましたのが、核兵器という、最先端の物理学の産物でした。そのもっとも基礎の部分に「ミンコフスキー」というロシア（当時はソヴィエト連邦）風の名前（実際にもソ連圏のリトアニア生まれでした）が出てくることは、西側の技術者にとりましては大いに不愉快なことであったでしょう。だから、ミンコフスキーに代えてローレンツを持ってくる、まあわからない話でもないのですね。
ファインマンは、1963年に行なわれた講演（「科学は不確かだ」に収録）で、学問の価値を政治的に決めるソヴィエト連邦を非難しているのですが、もし政治的理由でミンコフスキーからローレンツへの切り替えがおこなわれていたのであれば、この言葉は米国にも向けられた言葉と解釈すべきでしょう。（同書は、本ブログの別記事でご紹介しています。）
いずれにせよ、今では冷戦も過去の歴史となり、ミンコフスキーの名におびえる必要はなくなりました。ならば物理法則は、よりシンプルな形に書き直した方が良い。ローレンツ変換に対して不変な形に式を書くよりも、時間を虚数として普通に式を書き下すほうが、よほど簡単ですし、物理学の進展にも寄与するでしょう。
なぜさっさとそうしないか、私には理解ができません。まあ、さほど遠くない将来、そうした動きが起こるであろう、とは想像しているのですが、、、
時間軸のみが虚数的に振る舞う理由
さて、最後に、なにゆえに時間軸のみが虚数的に振る舞うか、という点に関して少し考察を加えておきます。
このブログでも「時間のなぞ」と題して書いたのですが、全ての観測者の意識は速度1（別の言い方をすれば、時速1時間）で四元時空の中を未来に向かって時間軸方向に進んでいます。
互いに運動している観測者が他の観測者を見れば、相手は空間的な速度も持っており、これと時間方向の速度との合成速度が彼の速度ということになります。で、これを合わせた四元速度は、それぞれの座標系に固定された観測者にとっては時間軸に他なりません。
つまり、時間軸は、互いに相対運動する観測者毎に、異なる方向を向いております。
時間軸がそれぞれの観測者にとって異なる方向を向いている、ということは、四元時空の時間軸が他の空間軸と異なる振る舞いをする（時間軸のみが虚数的に振る舞う）原因が四元時空そのものにあるのではないということを意味します。
四元時空の特定の方向が虚数的な振る舞いをするのであるなら、観測者ごとに時間軸の方向が異なることなど、あり得ないはずです。
時間軸の方向が観測者に依存する以上、時間軸が他の空間軸と異なる振る舞いをする原因は観測者にある、と考えざるを得ません。
四元時空は等方的であって、四元時空自体には時間軸と空間軸の区別はなく、時間軸と空間軸に異なる性質を与えているのは観測者自身である、と考えるのが妥当でしょう。
観測者の意識は、時間軸方向に速度1で移動しながら、それぞれの時刻に対応する三次元空間を切り出して観測しています。つまり、観測者にとっての時間軸は、切り出した空間に直交する方向であり、他の空間軸とは明瞭に区別されます。
食パンをスライスすれば、食パン自体は等方的なものであっても、切り出されたパンの面内の方向と面に垂直の方向は明らかに異なる性質を持ちます。切り出された面内方向にしかバターは塗れないのですね。
同じことが、観測者の観測する時空においても生じているのでしょう。そして時間軸と空間軸の違いが、虚数的振る舞いと実数的振る舞いの違いとして観測されるのでしょう。
なぜそれが、実数と虚数の違いとなって表れるのか、これはまだまだ「なぞ」としか言いようがないのですが、、、
2018.3.25追記：空間軸と時間軸の虚実を反転させるのは、切り出された三次元空間と時間軸が直交していなくてはいけないという要請に応える一つの解ではあります。ただし、虚数でなければならぬ、とは言えません。つまり、充分条件ではあるが、必要条件ではない、ということですね。他に解がないのであれば、消去法でこれだ、ということになるのですが、、、
ちなみに、虚数（複素数）によく似たものに四元数というものがあります。四元数は4つの実数に対応しており、四次元空間によく対応しているようにも思えますし、一つの実数と三つの虚数が含まれることから、ミンコフスキー空間の虚実を入れ替えたものに対応しているようにも思えます。でも、四元ベクトルと四元数は、空間軸の同等性に関して少々矛盾した部分があるようにも思えます。このあたりは、もう少し考察が必要な部分でしょう。
2018.4.29追記：四元数の三つの虚数成分は、ii = jj = kk = ijk = -1の関係を満たすのですが、この式からijkの規定を外して、ij = jk = ki = ijk = 0とすれば、四元ベクトルを一つの四元数で表すことができます。ただし、四元数のijkの規定にはそれなりの理由があるはずで、いくら四元ベクトルと対応がとれるといっても、この条件を変更できるかどうかは、疑わしいような気も致します。
2018.4.15追記：なぜ時間が虚数的に振る舞うか、という問題に解が得られたように思います。まあ、解が得られたというよりは、昔からわかっていることであったことに気付いた、ということなのですが。
つまり、特殊相対性理論がそれを要請している、ということなのですね。だから、四元時空がミンコフスキー空間でなければならないこと、時間が虚数的に振る舞うことは、最初からわかっていたことだったのですね。
時間が虚数的に振る舞うための前提は、物理法則がいかなる慣性系でも同等に成立していることと、その物理法則が一つの速度を導き出しているという二点が要請されます。この程度の要請であれば、認めても良いように、私には思われます。
ちなみに、この「物理法則から導き出される一つの速度」は、具体的にはマクスウェル方程式から導かれる光速です。また、この速度が許容される最大速度になるというのが特殊相対性理論の結論の一つでした。
4/16追記：上の説明は、大域的な説明で、おそらくは、局所的な説明が別にあるものと思われます。
大域的な説明とは、エネルギー保存則のようなものであって、これまでエネルギー保存則に反する現象は見出されていないのですが、これは様々な物理現象が、なぜかエネルギー保存則を満足する形にできているからそうなるのであって、それぞれの物理現象は個々に（エネルギー保存則とは別の形で）説明がなされております。
エネルギー保存則は、ネーターの定理により、時間方向の対称性が成り立つ場合にエネルギーは保存されなくてはいけないこととなります。物理法則が異なる慣性系でも同じように成り立つという要請も一つの対称性ですから、これから時間の虚数性が要請されるということは言えるのでしょう。ただし、時間が虚数的に振る舞う理由は、別に何かあるものと思われます。それが何か、これが当面の問題です。
天動説対地動説との類似性
上のように見てまいりますと、ローレンツ変換とミンコフスキー空間の違いは、天動説と地動説の違いとよく似ております。どちらがより単純に現象を説明できるか、これを考えればいずれの見方をすべきかは、おのずと結論が得られるのではないかと思います。
天動説と地動説は、それほど異なるものではない、ということをMechaAG氏が書かれております。むしろ大きな違いは、天体の運動が円軌道か楕円軌道かという問題であって、そういう意味では、コペルニクスよりもケプラーの方が大きな仕事をした、というのですね。
たしかに、数式上、あるいは、数値上では、ケプラーの仕事の方が大きい。でもここで問題になっているのは、世界観、なのですね。つまりは、この大地は、微動だにせぬ、確固たる存在であるのか、宇宙空間を漂う土塊なのか、という問題ですね。
この問題と時間が実数なのか虚数なのかという問題は、比較的似ている。表象と物自体を同一視するなら、時間は実数と言わざるを得ない。人の精神内部にできた世界と、人とは無関係に存在する世界を異なる世界であると認めることができるなら、時間を虚数とみなすこともできるのですね。
ここに、カントとデカルトという、巨人たちの歩んだ一歩がある。その一歩が、相対論や量子論をサポートすることに、私はある種の感慨を覚えているのですが、それが人類の多くに共有される日ははたして来るのかどうか、最近では自信がなくなってまいりましたことも、また事実ではあります。ま、このあたりはどうでもよいことですから、あまり深刻に悩んでいただく必要はないのですが、、、
MechaAG氏のもう一つのエントリーでは、「天動説と地動説は数学的には等価で変換できるんですよ。だからどっちも正しい。あくまで数学的には、ね。」と書いたあとで、ハムスター速報の天動説と地動説の違いを説明するGIFを紹介されています。
たしかに、天動説でも周転円*を用いることで複雑な惑星の軌道も説明することができます。地動説でも、じつは、天体の軌道は円軌道ではなく楕円軌道であるため、数が少ないとはいえやはり周転円は必要になるのですね。
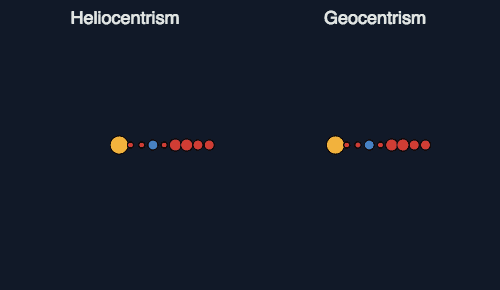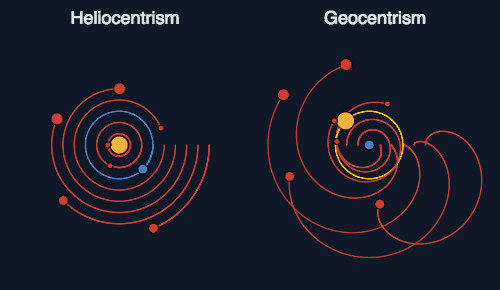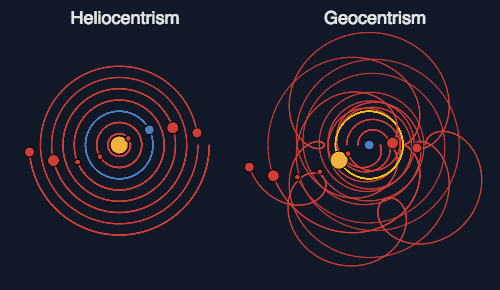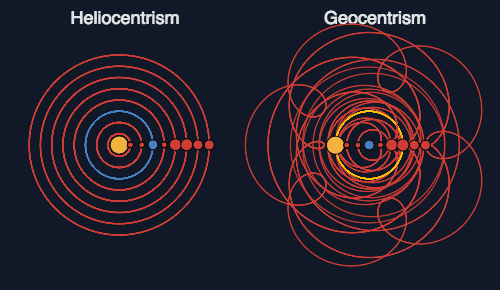
そうなりますと、天動説と地動説、いずれが間違っているとも言い難い。自然現象の説明がよりエレガントなのはどちらであるか、ということが、いずれを選ぶかの判断基準になるでしょう。そして、コペルニクスやガリレオに軍配を上げるのであれば、時間の扱いをどうすべきかも、おのずと決まってくるのではないか、と私などは思ってしまうのですね。
まあ、このあたりは、いずれ人々も気づくのではないかと思いますが、、、
*：周転円とは、惑星の軌道を大きな円軌道（従円）を回る点を中心とする小さな円軌道（周転円）上に惑星があると見做すことで、惑星の複雑な運動を説明するもの。フーリエ級数展開と同様な効果を持ち、円の数を増やすと極めて複雑な運動も説明できます。
ミンコフスキーの扱いは、時間座標と空間座標の間に虚数・実数の関係がある、とするだけで時間と空間を統一的に扱うことを可能としています。これは、惑星は恒星の周りを円軌道を描いて回るとするコペルニクスの主張に近い考え方なのですね。
一方のローレンツ変換では、変換公式の他に、四元ベクトルのスカラー積を演算する際に、空間項と時間項で符号を反転する等の、余計なルールを付け加える必要があります。
これは、時空が虚実の関係にあるならあたりまえのことなのですが、ローレンツ変換は、時間も空間も実数であるとして扱っているため、この部分での符号反転を新たなルールとして導入する必要があります。
その他、量子力学の公式のあちこちに現れる虚数単位は、時間を虚数とすることで消えてしまう。量子力学への虚数の導入は、時間が虚数的に振る舞うとすれば、極めて自然な形に導入されます。
そればかりか、量子力学で波動が生じる原因が時間の虚数性によるとも考えられるわけで、物理現象をより単純な法則で説明することができるようになるのではないかと思われます。
（この節は、追記の形で書き加えたものを独立の節にまとめ直したものです。また、別記事にまとめを行っております。最新のまとめ「虚数時間とファインマン氏の憂鬱」も、ぜひどうぞ。）
こんばんは
記事を読んで頭の中のモヤモヤ【各種計算の全体的なイメージが掴めない】
が少し解消した気持ちになりました。ありがとうございます。
負数や虚数などの歴史的（現在も）な問題点の原因は、数や計算というものが
生成過程の全体ではなく部分しか表現されていない為であると思うのです。
例えの整合性がいまいちだと思いますが、地（全）動説が全体で天動説は
地を固定した、全動説の部分だったように・・・。
部分でも明確な矛盾が無ければ自然法則を記述する事はできると思います。
しかし、全体的視点に立つとモヤモヤが発生するような気がします。
数や計算が生成された時代は脳の中については殆ど解っていないと思います。
しかし現在は、人が何かを考えると脳内の状態が変化するという事が画像として捉えられています。
また、数は人によって抽象されたものであるという認識が普及しています。
以上より、数や計算を脳内の変化として考査してみます。
「 」以後この「」内の状態を、数等を考えていない状態とします。
「● 」●←人が何らかの対象に対して１と対応付けした状態とします。
「●● 」別の同類の対象に対して１と対応付けした状態とします。
「(●●) 」その全体を１に対応付けたものを、２と対応付けます。
ここで、２－１＝１という古来からの演算を考えてみます。
α「●● 」－「● 」＝β「● 」となります。
α「●● 」２から１を引くと
β「● 」１になるという自明な結果が表現されています。
しかし、その過程を眺めてみると、確かに●は一つ無くなっていますが、
●に相当する「 」内の白い部分は増加（演算では＋と表現）しています。
しかし、２－１＝１ にはその状況の説明は存在していないと思うのです。
また、a＜b のとき a から b は引けないと数学では説明していますが、
「 」という前提が存在しなければ１だって足せない筈です。
現在の数や演算には以上についての表現が欠けていると思います。
虚数というのは「 」の白い世界での掛け算のような気がします。
数学の専門家であれば、全体的な状況というものを把握しているからいいのですが、多くの高卒者にとって、現在の数学教育というものは、自然の真理的存在から派生した心という存在に、人の我儘を押し付けているとしか思えません。
佐藤さん、コメントありがとうございます。
このコメントに対する充分な返答になっているかどうか、多少疑問ではありますが、このコメントを読んで思いましたことを「数という概念と加納朋子著『スペース』の困惑」というタイトルの最新記事に書きました。ご参考までにどうぞ。